


| home |
Redan 1820 upptäckte Hans Christian Örsted (1777 - 1851) att en strömgenomfluten ledare påverkade en kompassnål i en kompass. Det bildades ett cirkulärt magnetfält med riktning enligt skruvregeln eller tumregeln.
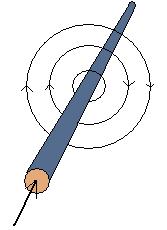
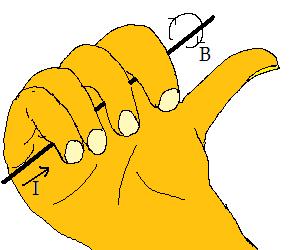
Magnetfältets storlek benämns magnetisk flödestäthet och beteckans B [T] tesla.
Enheten T tesla är uppkallad efter Nikola Tesla (1856 - 1943)
Magnetiska flödestäthetens storlek bestäms med formeln för flödestätheten B
B = μo · I / (2πr)
μo = 4π·10-7Wb/Am, I = ström, r = avstånd från ledaren.
Det bildas ett magnetfält kring en strömgenomfluten ledare. Är ledaren i ett annat magnetfält, kommer magnetfälten att adderas med riktning. Till vänster om ledaren kommer magnetfälet i bilden att förstärkas, till höger om ledaren kommer magnetfältet att försvagas.
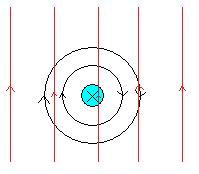
Naturen vill ha jämnt och fint magnetfält överallt och strävar efter att utjämna. Det innebär att naturen vill flytta ledaren åt höger för att jämna ut. Det uppstår en kraft F riktad åt höger på ledaren. Kraften beror av strömmen genom ledaren I och hur lång ledaren är i magnetfältet L samt magnetfältets storlek.
F = B I L
Magnetfältets riktning, strömriktningen och kraftens riktning ska vara vinkelräta enligt högerhandsregeln.
En ledare som det går ström genom skapar ett magnetfält kring ledaren.
Placerar man en annan ledare på avståndet r från den första ledaren som det går ström genom, kommer den nya ledaren att påverkas av magnetfältet från den första ledaren.
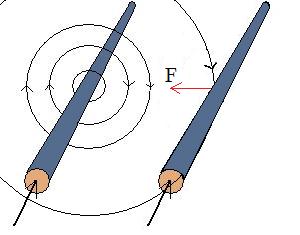
Kraften på en längd L av den högra ledaren blir
F = B I2 L
där I2 är strömmen i den högra ledaren och B kommer från den vänstra ledarens magnetfält.
B = μo · I1 /(2πr)
ger
F = μo · I1 /(2πr) · I2 · L
Om båda strömmarna går inåt kommer magnetfältet från den vänstra ledaren att vara riktat neråt där den högra ledare befinner sig. Högerhandsregeln ger då att kraften på den högra ledaren är riktad mot den vänstra ledaren.
Den högra ledaren skapar ett magnetfält där den vänstra ledaren befinner sig. Kraften på den vänstra ledaren blir då riktat mot höger.
Kraft och motkraft är lika stora och motsatt riktade.
Två strömgenomflutna parallella oändligt långa ledare påverkar varandra med kraften F = 2.00·10-7 N per meter av ledaren, om de är på avståndet r = 1.00 m och strömstyrkan i ledarna I = 1.00 A.
Detta är definitionen för strömstyrka I som mäts i ampere uppkallad efter André-Marie Ampère (1775 - 1836).
Magnetfältet kring en strömgenomfluten ledare är cirkulär vinkelrätt mot ledaren. Om ledaren böjs ihop till en cirkel kommer magnetfälten att adderas inuti cirkel och bilda ett nästan homogent magnetfält.
Rullar man ihop ledaren till många varv får man en spole.
Riktningen på magnetfältet i spolen fås med hjälp av en variant av tumregeln.
Lägger man höger hand runt spolen med fingrarna i strömmens riktning kommer tummen att peka i magnetfältets riktning inuti spolen.
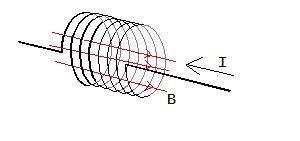
Flödestätheten B inuti spolen kan bestämmas med formeln
B = μ·N·I / L
där μ = permeabiliteten, N = antal varv i spolen, I = strömmen i spolen, L = spolens längd
Om spolens längd är liten och alla varv är tätt sammanhållna kallas spolen platt. Flödestätheten i en platt spole bestäms med formeln
B = μ·N·I / d
där μ = permeabiliteten, N = antal varv i spolen , d = spolens diameter.
Går det ström genom en ledare i ett magnetfält uppstår en kraft på ledaren. Strömmen består av laddningar som rör sig i ledaren. Det är den rörliga laddningen som är upphov till den magnetiska kraften på ledaren. Strömmen av laddningar beror på laddningarnas hastighet och laddningarnas storlek. Kraften blir
F = Q v B
där Q är laddningens storlek, v = laddningens hastighet och B är magnetiska flödestätheten.
Kraftens riktning bestäms med högerhandsregeln. B, v och F ska vara vinkelräta mot varandra.
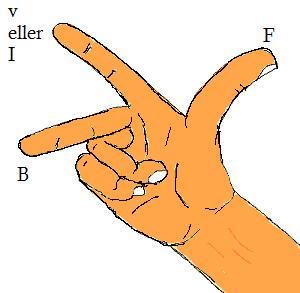
En partikel med laddning Q och hastigheten v kommer in i ett magnetfält med flödestätheten B. Partikeln påverkas av en kraft F.
F = Q v B
Denna kraft är vinkelrät mot hastigheten och magnetfältet. Vinkelrätheten innebär att kraften inte påverkar rörelseenergin utan bara hastighetens riktning. Partikeln börjar röra sig i cirkelbana.
Kraften för att hålla en partikel i cirkelformad bana är
Fc = m v² / r
Denna kraft kommer från magnetfältet
Fm = Q v B
vilket ger
m v² / r = Q v B
Dividera båda leden med v, multiplicera båda leden med r.
m v = Q B r
Kvadrera ekvationen
m² v² = Q² B² r² (ekvation 1)
Partikeln har hastigheten v som den kan ha fått genom acceleration av spänningen U. Rörelseenergin hos partikeln är
Ek = m v² / 2 = Q · U
Lös ut m v² ur ekvationen ovan.
m v² = 2 · Q · U (ekvation 2)
Tag nu ekvation (1) och ekvation (2)
m² v² = Q² B² r² (ekvation 1)
m v² = 2 · Q · U (ekvation 2)
Dividera dem med varandra
m = Q B² r² / (2 U )
Med detta uttryck kan man bestämma partikelns massa. Om laddningen är en elektron kan vi få fram elektronmassan me.
Om laddning Q, spänningen U och magnetfältet B hålls konstanta kommer massan att vara proportionell mot radien². Man kommer att få olika radier för partiklar med olika massor. Detta används i masspektrometern för att bestämma massor på atomjoner.
En laddad partikel med hastigheten v kommer in i ett elektriskt fält. Den påverkas då av en kraft
FE = Q · E
Lägger man på ett magnetiskt fält vinkelrätt mot elektriska fältet kommer partikeln också att påverkas av en magnetisk kraft
Fm = Q v B
Med lämpliga värden på E och B kommer krafterna att vara lika stora
FE = Fm
eller
Q · E = Q v B
Krafterna är lika stora om hastigheten v = E / B
Partiklar med hastigheten v kommer då att gå rakt fram och partiklar med andra hastigheter kommer att böjas av. Vi har fått ett hastighetsfilter för laddade partiklar.
| home |